README.md

695. Max Area of Island

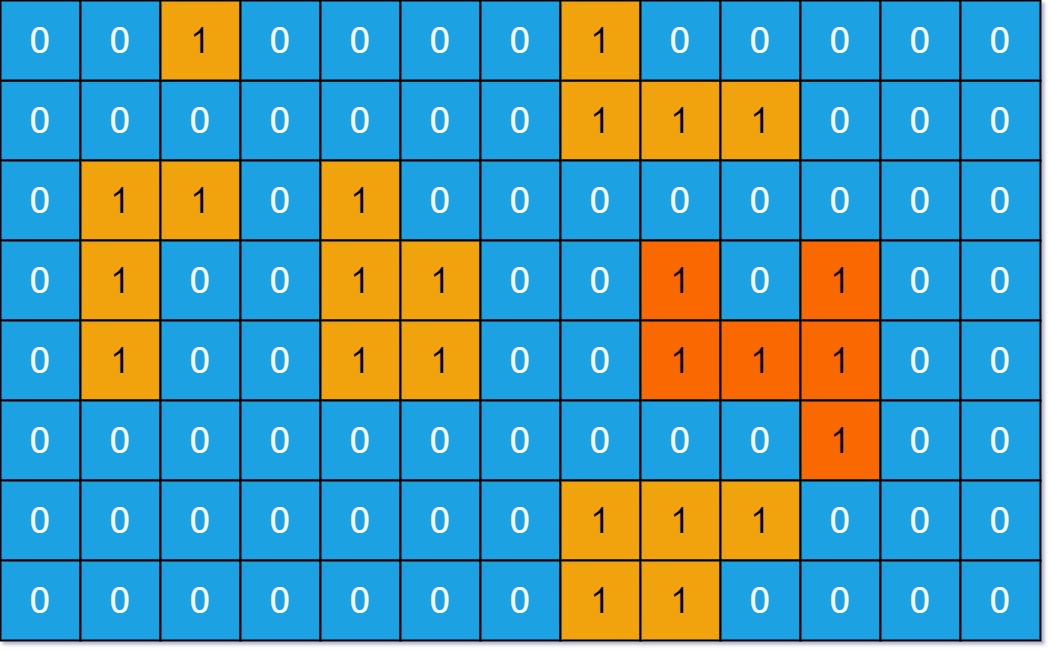
You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.

The area of an island is the number of cells with a value 1 in the island.

Return the maximum area of an island ingrid. If there is no island, return 0.

Example 1:

Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]] Output: 6 Explanation: The answer is not 11, because the island must be connected 4-directionally. 

Example 2:

Input: grid = [[0,0,0,0,0,0,0,0]] Output: 0 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• grid[i][j] is either 0 or 1.

Solutions (Ruby)

1. DFS

# @param {Integer[][]} grid# @return {Integer}defmax_area_of_island(grid)m=grid.sizen=grid[0].sizeret=0(0...m).eachdo |i| (0...n).eachdo |j| nextifgrid[i][j] == 0area=0cells=[[i,j]]untilcells.empty?i,j=cells.popnextifgrid[i][j] == 0area += 1grid[i][j]=0cells.push([i - 1,j])ifi > 0 && grid[i - 1][j] == 1cells.push([i + 1,j])ifi < m - 1 && grid[i + 1][j] == 1cells.push([i,j - 1])ifj > 0 && grid[i][j - 1] == 1cells.push([i,j + 1])ifj < n - 1 && grid[i][j + 1] == 1endret=[ret,area].maxendendretend

Solutions (Rust)

1. DFS

implSolution{pubfnmax_area_of_island(mutgrid:Vec<Vec<i32>>) -> i32{let m = grid.len();let n = grid[0].len();letmut ret = 0;for i in0..m {for j in0..n {if grid[i][j] == 0{continue;}letmut area = 0;letmut cells = vec![(i, j)];whileletSome((i, j)) = cells.pop(){if grid[i][j] == 0{continue;} area += 1; grid[i][j] = 0;if i > 0 && grid[i - 1][j] == 1{ cells.push((i - 1, j));}if i < m - 1 && grid[i + 1][j] == 1{ cells.push((i + 1, j));}if j > 0 && grid[i][j - 1] == 1{ cells.push((i, j - 1));}if j < n - 1 && grid[i][j + 1] == 1{ cells.push((i, j + 1));}} ret = ret.max(area);}} ret }}